“The thing is, bad questions don’t destroy the community. […] But this hostile behavior does destroy the community. It pushes beginners away, who may ask better questions later once they get a bit more of a handle on what they’re doing. And it pushed people like me away; people who are there to help, and willing to do so even for beginners.” — lambda on Hacker News
Despite saying that I was not going to learn how to code, I’ve been playing around with Learn Python the Hard Way. The author has a smart practice of posing questions to the student as quasi-homework — your job is to Google around until you find the answer. Thus you build the habit of solving puzzles via research.

In the “Study Drills” section of the fifth exercise, the author instructs, “Try more format characters. %r is a very useful one.” I suspect I’m not the only student who instantly searched “Python format characters”. One of the first results was a page from the Python 2 docs. The answer was in there, but I didn’t realize that because it was way the hell down the page (here). The top of that page said this, which I found incomprehensible:
“The principal built-in types are numerics, sequences, mappings, files, classes, instances and exceptions.
Some operations are supported by several object types; in particular, practically all objects can be compared, tested for truth value, and converted to a string (with the repr() function or the slightly different str() function). The latter function is implicitly used when an object is written by the print() function.”
I read that and thought, “Well, this must not be what I’m looking for!” Back to Google. The next place I went was a Stack Overflow question:
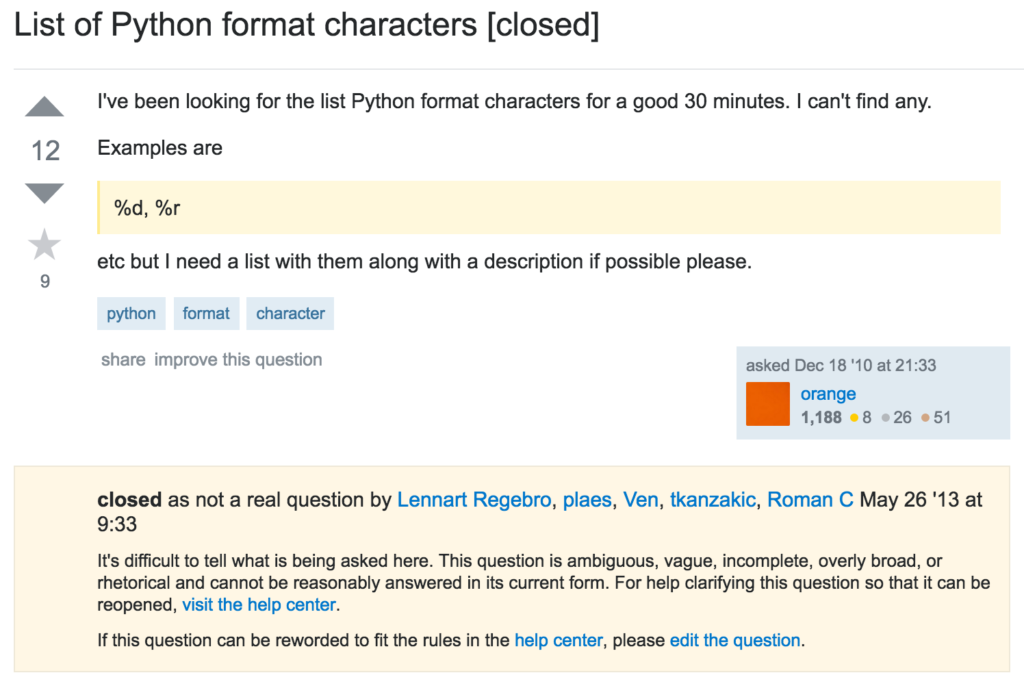
Aha! Someone had the same problem I did! (Granted, I was a couple minutes into my search, not thirty, but the original post was from 2010.) Underneath the request for help, a closure note called this… “not a real question”? Hmm, okay. I guess the OP didn’t follow all the “You Must Try, and then You Must Ask” rules (which I wholeheartedly believe in, and to which Stack Overflow’s guidance seems similar) — but it was pretty clear what they were looking for.
I scrolled down to read the answers. This was the first one, ranked by upvotes:
“Here you go, Python documentation on old string formatting. Took me one minute to find (tutorial -> 7.1.1. Old String Formatting -> ‘More information can be found in the [link] section’), something must be wrong with your search strategy ;)” — user delnan
This is helpful because it provides the desired information. But it profoundly fails to empathize with the beginner’s struggle. I suspect that the person who asked this question, like me, found that docs page easily. It was just totally non-obvious that the answer was in there! I appreciate the third Stack Overflow response, which has a tenth of the first one’s upvotes:
“In docs.python.org Topic = 5.6.2. String Formatting Operations http://docs.python.org/library/stdtypes.html#string-formatting then further down to the chart (text above chart is ‘The conversion types are:’) [¶] The chart lists 16 types and some following notes. [¶] My comment: help does not include attitude which is a bonus. The attitude post enabled me to search further and find the info.” — user oceandreamer
Another user, Lennart Regebro, commented, “The first hit [on Google] is now tragically this stupid question” instead of the Python 2 docs page. Well, the docs didn’t help me at all without access to “this stupid question” and the explanations it provoked. Because you don’t know what you don’t know — reading the top of that docs page made me think it had nothing to do with what I was looking for. Yes, I was wrong, but that’s because I’m a goddam beginner! By definition I’m not good at parsing technical documentation!
If your answer to this problem is “read the entirety of every docs page to make sure there is no relevant section”, you’re being totally unrealistic — it’s just not going to happen. Maybe the original asker and I should have done ctrl + f for r% — but that didn’t occur to me, so I assume it didn’t occur to them either.
Beginners need guidance. They’re dumb and they flail around and they get stuck on “easy” problems. That’s why resources like Learn Python the Hard Way and Stack Overflow exist in the first place.
I don’t think the docs of a programming language should be tailored to newbies who have no idea what they’re doing. That would be silly. I do think that people who participate in learning-oriented spaces should not answer questions with this jaded, snarky, put-upon air. It is the opposite of welcoming and it does nothing to make me feel delighted about talking to programmers. But hey, if you don’t want a friendly community or you don’t want more people to learn how to code, then you’re doing it right.
I quoted Hacker News user lamdba at the beginning, but their comment is so good that you should really go read the whole thing.